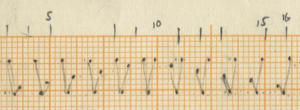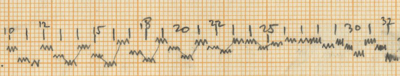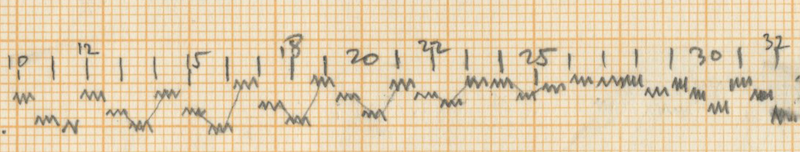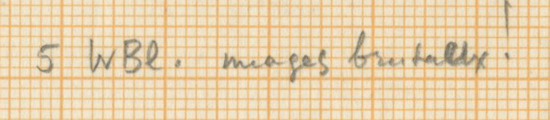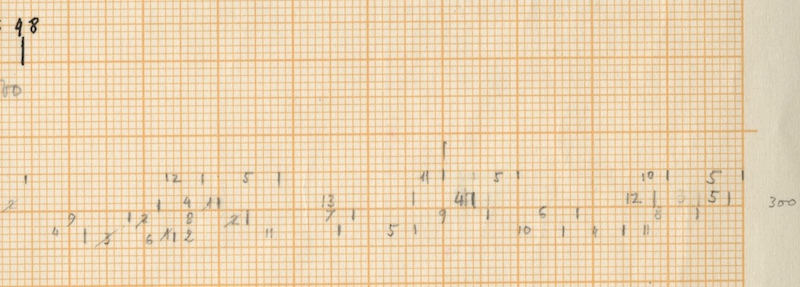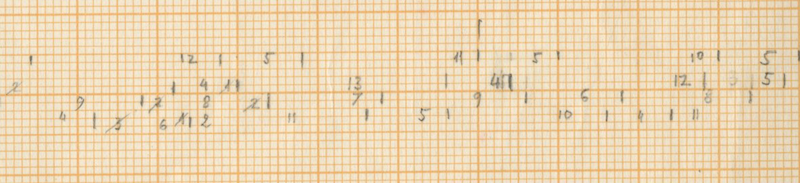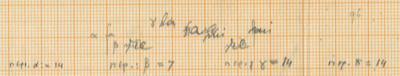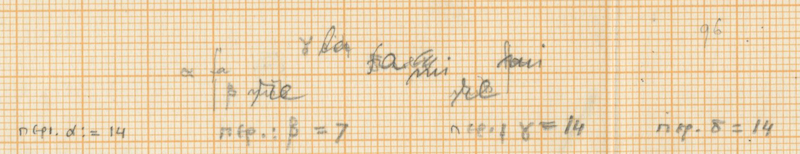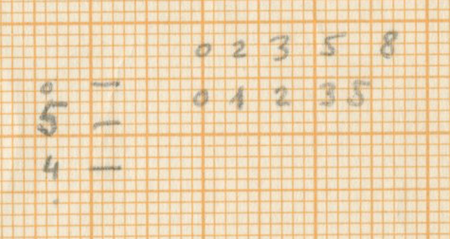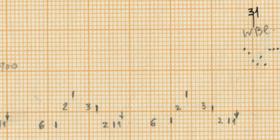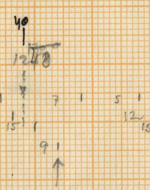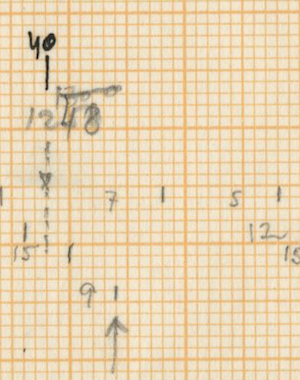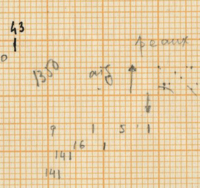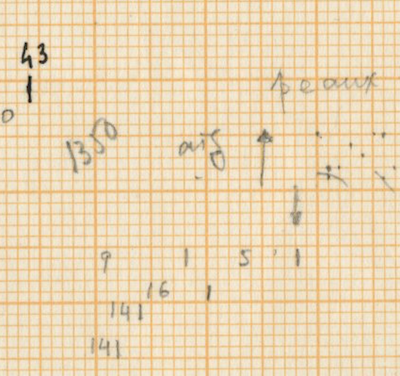Living Scores Learn

Improving the practice and performance of contemporary music

Meso structure

all examples on this page are published with permission of collection Famille Xenakis. DR. and may not be copied unauthorized without permission.

Rebonds A

Display mode
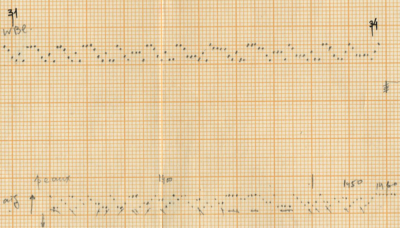
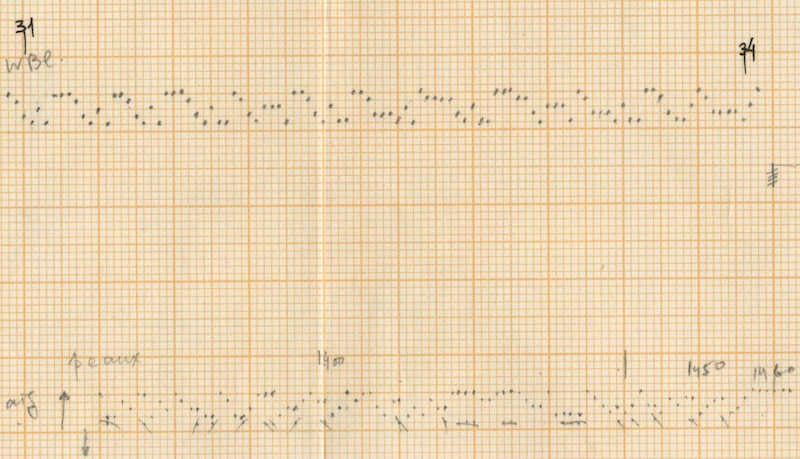
Rebonds A seems to be written very intuitively, without making use of calculations or mathematics of any kind. As we stated above Xenakis seems to have composed only the first 50 measures of the piece in his sketches and then added the final ten bars at a later time. Because Xenakis applies sieves (See chapter below: “Sieves”) to the musical material, of course a lot of the generated material appears as scales or seems to be simply “displaying” the instruments within one piece. This is absolutely the case in Rebonds A: according to us, the development of the piece is based on a “display” approach of the setup. This is clear in two ways. Firstly, it is demonstrated in displaying the consecutive instruments in the setup (e.g. it is very clear in the use of the anapestic element but also later on in the other of the seven elements): every new element that he introduces implies a “run-through” of the set-up.
Secondly, it is shown in what we call the “noise” part of the piece (1). The same method of scaling is followed in presenting the material. The different elements are “displayed” in the same consecutive manner: Xenakis starts with the iambus element, then the anapest, and then gradually moves through the other elements into the middle part that consist only of the “noise” part of the seventh element. From bar 34 onward (quarter note 132-133), he starts inserting the initial elements again until he reaches the point that only multiples of separate instruments still stand in the last measures.
Accents
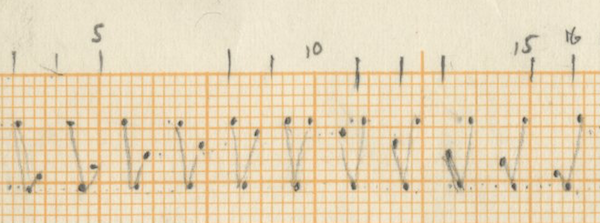
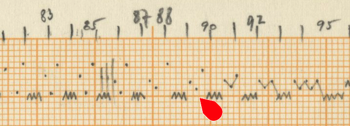
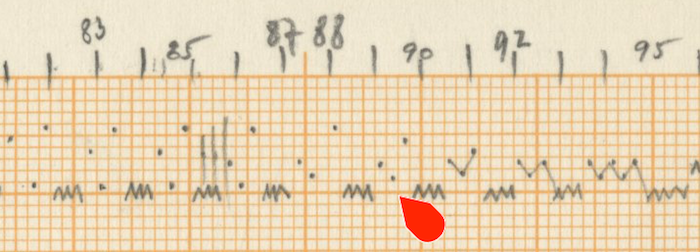
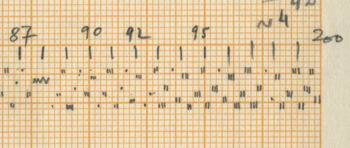
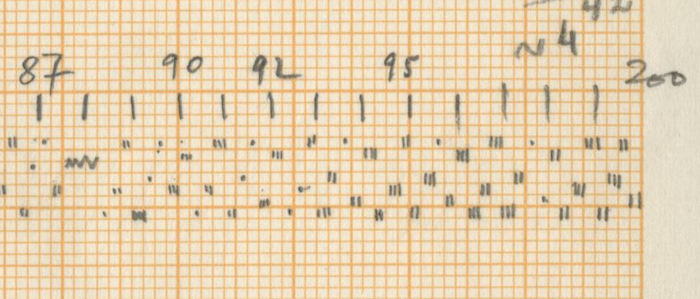
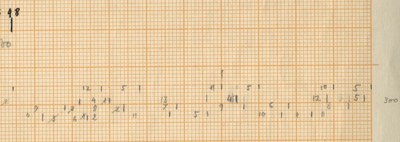
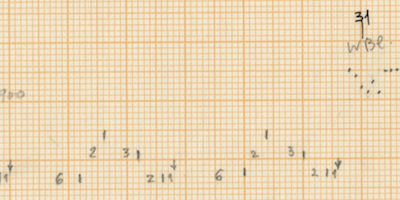
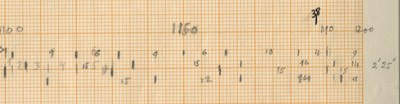
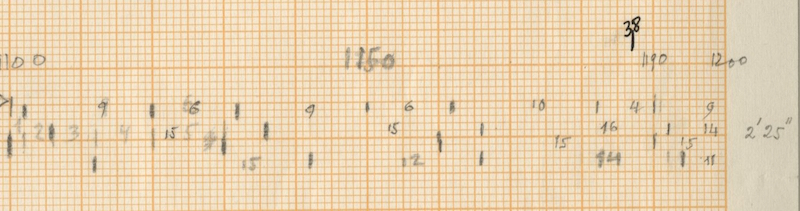
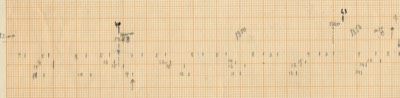
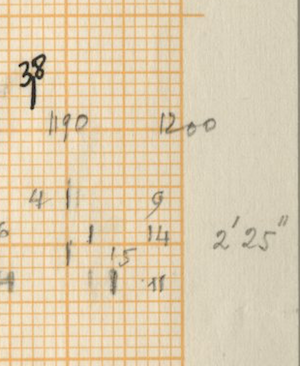
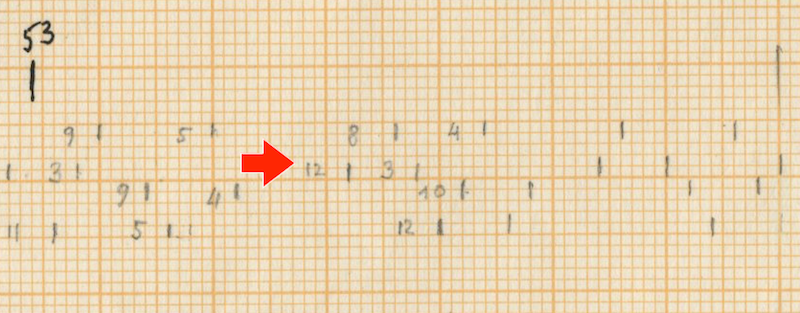
After counting the frequency of the single accents in Rebonds A, the series that comes out is possibly connected to a complex sieve series. Since the composer did not leave any trace of the calculations of this particular sieve, it is quite impossible to know the exact series used. One thing stands out clear from the list: towards the end of the piece, the density of the accents rises and their frequency is raised up to 6 times if we compare with the accent frequency in the beginning of the piece. The double accents seem to mark important structural decisions in the piece. For example, the first double accent appears when the high bongo is not used anymore in the musical context as part of the initial written out line (measure 23).
Of course the high bongo appears again in measures 24-25-26, but here it is used as ornamentation through polyrhythms of the original line of the sketches. The second double accent appears when this high bongo appears again as a musical element after the “noise” section and is followed immediately with a double accent in the medium tom to “prove” this statement.
From measure 38 onward (quarter note 149), the double accents mark every new entry of one of the composed musical phrases.
Fibonacci
For the “Golden Section analysis issue” that appeared in Percussive Notes Magazine (20) stating that the piece’s axis of rotation lies in measure 23, this point is close to 0,382 of the piece and could mark the first appearance of the double accent as well. Another hypothesis in this sense may be the 0,618 point of the piece that is quite close to the beginning of the double accent phrases that start in measure 38. Perhaps the Golden Section was also applied to the actual 200 composed quarter notes in the way that it follows the point in the piece where the “elements” take over from the noise again, i.e. quarter note 133: 200 x 0,618 equals 123,6. So this point in the composition seems the closest. All of this, however, is very arguable.
Density and polyrhythm
The density clearly rises through the piece until quarter note 200. The polyrhythms in the score seem to be added afterwards and seem to add to the rising density of the piece. In the sketches we could not find any trace of polyrhythmic writing except for a small note of 3 over 2 above quarter note 48 (example of sketches), but this does not seem to have anything to do with this particular measure. Especially in quarter notes 188 until 200 in the sketches, this issue stands out very clear: the extremely present polyrhythms of the final score do not appear in the sketches at this point.

Rebonds B

Display mode
Xenakis applies the same “scaling of instruments” in Rebonds A, as mentioned above, to Rebonds B: all instruments are clearly “displayed” in a consecutive manner. This is especially the case in the fast woodblock and tom section (called “nuages bruiteaux” by Xenakis in the sketches) and in the pianissimo tremolo section until the end. These sections (“nuages bruiteaux” and the section from the pianissimo tremolo in measure 65) also seem to be written quite intuitively and without the implementation of calculations.
Bell tower effect theory
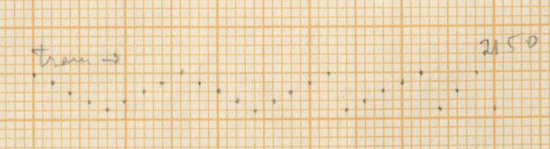
As stated in the thesis of Barthel, there is a motive linked to a traditional Greek Church bell from the Monastery of Aghia Lavra in the Peloponnesos (3) accelerating and slowing down again. We find a stunning example of this bell imitation in Rebonds B in measures 48 until the pianissimo tremolo in measure 65, here applied as four superimposed “bells.”

detailed example

In the beginning of the accelerando of the bells, all the voices have a short-long pattern (4).
While staying in Bologna, Italy over Easter some time ago, we heard the typical church bell competitions held in the area “displaying” the bells in different upward and downward scales. It is plausible that the superimposed four-against-five woodblock-skin passage at the very end of Rebonds B echoes the traditional church bell approach around the Mediterranean. This is a hypothesis of the author nevertheless.
Another hypothesis of the authors questions the musical aesthetics of the beginning of Rebonds B: it is possible that the beginning of Rebonds B echoes 4 to 6 church bells (6 church bells if you count the accentuated high bongo and it’s grace notes). Every instrument has it’s own speed. Due to differences in speed between the bells, the melody gradually changes (5).
Sieves
In the sketches, the theoretical sieves for each of the four entities are stated:
  • Instrument a: 14
  • Instrument b: 7
  • Instrument c: 14
  • Instrument d: 14
This order being the order of appearance: a is the tom, b is the bass drum, c is the bongo and d is the tumba.
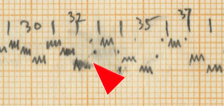
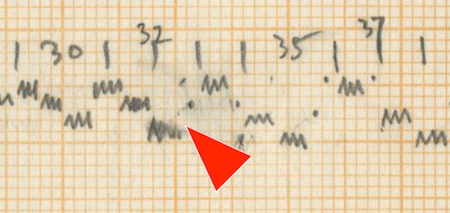
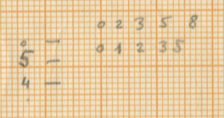
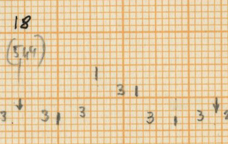
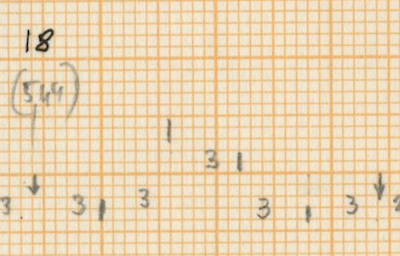
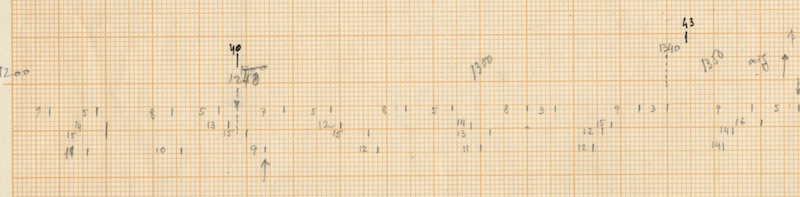
Xenakis distributes these instruments in a written out acceleration to organise them amongst each other. This acceleration is based on the series of Fibonacci, as stated in the sketches (He states 0, 2, 3, 5, 8 and 0, 1, 2, 3, 5 close to the theoretical sieves in the sketches). The 14 units of the initial sieve are divided in a residual value that differs every period (the first time 6 units, the second time 6, the third time 5 etc.) and the written out acceleration is mostly distributed as 2-3-2-1 with some exceptions.
This distribution gradually evolves to an overall distribution of 3 between all instruments in measure 18 and comes back to the initial distribution in measure 29 and 30 right before the first cloud of woodblocks.
In addition to the sieves applied to the four lower voices, the accents and grace notes in the high bongo also seem to be organized by sieves. Here, the accents begin with sieve 75 and the grace notes with 40. However, this is not documented in the sketches. For more information about sieves and their theory we refer to the article “Sieves” by Iannis Xenakis (6). The two moments where the high bongo is replaced as the “time-keeper” by the consecutive lower instruments (measures 8-9 and 16-18) do not interrupt the distribution of the instruments and are therefore no more than an interruption of the basic high bongo pattern. These moments have no structural influence.
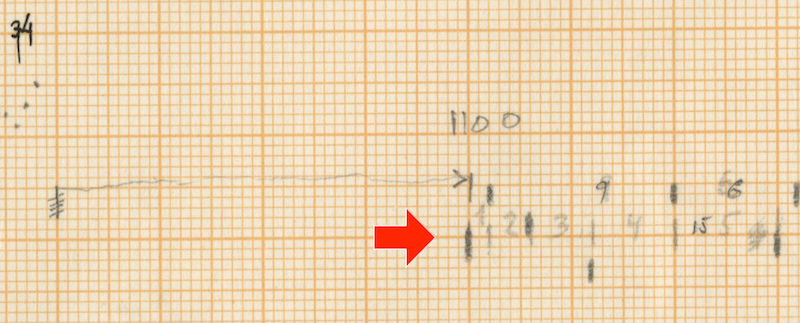
After the first “nuage bruiteau” in the woodblocks in measures 30-34, the low bongo becomes the voice with smallest distribution instead of the bass drum as before. This part in the piece is already preparing the “bell passage,” which starts after the second “nuage bruiteau” in the toms, with a short-long pattern (9-6, 9-6, 10-4, etc.). The rest of the instruments follow a distribution close to the initial 14 sieves.
From measure 48 to 54, all instruments follow a short-long distribution as prepared by the low bongo before. They gradually speed up internally until they reach measure 56 (32nd note pattern) and slow down after that towards measure 65 as mentioned above in the bell tower effect theory. The initial distribution of the instruments as we found in the beginning of Rebonds B is brought back from the second half of measure 62: 6-2-3-2-1.
Fibonacci
As we stated above in the Rebonds A analysis, there is little proof for the use of the Golden Section in Rebonds B, except for the distribution within the sieves. Some things are striking nevertheless:
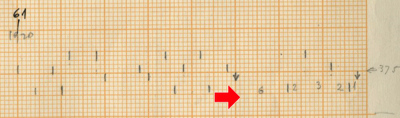
  • First section with the initial 30 measures: 30 x 0,618 equals 18,54: Almost exactly the point where all instrument distributions are 3.
  • The 0,618-point in the piece is exactly the point where the church bells start their acceleration to the fastest point. Xenakis marks this points in his sketches with a pencil mark, so it is possible they have something to do with the structure of the piece
There are more examples of these marks:
  • Mark in measure 38: all the instruments are very close and even together at some points
  • Mark in measure 40: Descending melody in the lower 4 voices
  • Mark in Measure 43: almost all distributions are 14 here and the grace note sieve in the high bongo speeds up significantly
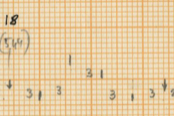
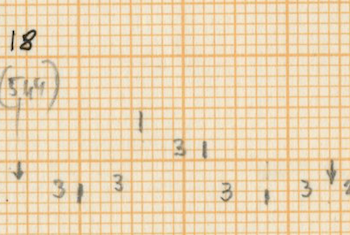
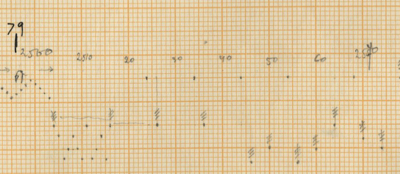
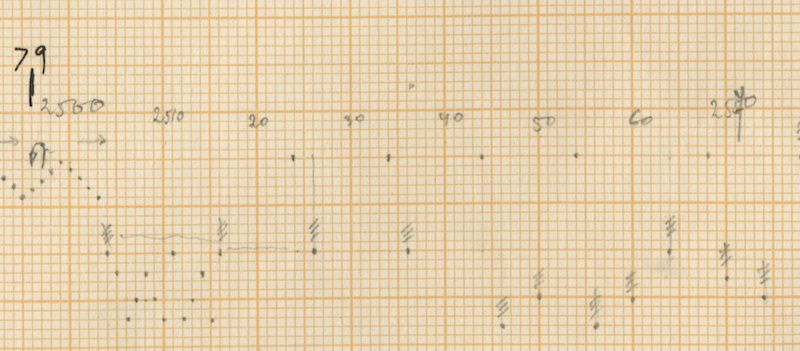
  • Ending of Measure 79: the point where the woodblock begins single interventions equals 0,618 of the section from the pp woodblock tremolo until the end (measure 65-end)
Mistakes in the printed score after reviewing sketches and manuscript score
Final sketch remarks
These are the translations of Xenakis remarks on the final sketch of Rebonds B:

“4 entities, each one with it’s own rhythm. They have given distances to one another. Mirror Images. Symmetries. The tones: a higher instrument, but of the same texture as the entities, skin for example.”

“Displacing the tones and the internal speed amongst the instruments:

  • A: based on only the periods of the 4 entities with independent displacing.
  • B: based only on the fluctuation between fa-mi bemol-si/sol bemol-mibemol-fa with an acceleration for example 3-1-2-1-0, thus changes of period (faster)”

Notes

Text written by Tom De Cock © Living Scores 2015
  1. Middle of measure 28 up to measure 34; quarter notes 110-132 in the sketches.
  2. BEYER, Greg, “All is Number, Golden Section in Xenakis’ “Rebonds””, Percussive Notes February 2005 pp. 40-50
  3. BARTHEL-CALVET, Anne-Sylvie, Le rythme dans l'oeuvre et la pensée de Iannis Xenakis, thèse de doctorat. Paris, Ecole des Hautes Etudes en Sciences Sociales, 2000, 2 vol., 700 + 482 p.: pp.468-469 mentions BALTENSPERGER, A., Iannis Xenakis und die stochastische Musik-Komposition im Spannungsfeld von Architektur und Mathematik, Anhang I: “Frühe Texte von Iannis Xenakis”, p. 607
  4. This maybe could be a reference to the iambic foot or could also be a reference to the actual sound of a hand-swung church bell: There’s always a loud beat and a softer beat.
  5. cfr. Phasing effect in the compositions of Steve Reich.
  6. XENAKIS, Iannis and RAHN, John , “Sieves”, Perspectives of New Music, Vol. 28, No. 1 (Winter, 1990), pp. 58-78